We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

The Graph of a Linear Function

Learning Outcome

  • Graph linear functions using tables
A helpful first step in graphing a function is to make a table of values. This is particularly useful when you do not know the general shape the function will have. You probably already know that a linear function will be a straight line, but let us make a table first to see how it can be helpful. When making a table, it is a good idea to include negative values, positive values, and zero to ensure that you do have a linear function. Make a table of values for [latex]f(x)=3x+2[/latex]. Make a two-column table. Label the columns x and f(x).
x f(x)
Choose several values for x and put them as separate rows in the x column. These are YOUR CHOICE - there is no "right" or "wrong" values to pick, just go for it. Tip: It is always good to include 0, positive values, and negative values, if possible.
x f(x)
[latex]−2[/latex]
[latex]−1[/latex]
[latex]0[/latex]
[latex]1[/latex]
[latex]3[/latex]
Evaluate the function for each value of x, and write the result in the f(x) column next to the x value you used. When [latex]x=0[/latex], [latex]f(0)=3(0)+2=2[/latex], [latex]f(1)=3(1)+2=5[/latex], [latex]f(−1)=3(−1)+2=−3+2=−1[/latex], and so on.
x f(x)
[latex]−2[/latex] [latex]−4[/latex]
[latex]−1[/latex] [latex]−1[/latex]
[latex]0[/latex] [latex]2[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]3[/latex] [latex]11[/latex]
(Note that your table of values may be different from someone else’s. You may each choose different numbers for x.) Now that you have a table of values, you can use them to help you draw both the shape and location of the function. Important: The graph of the function will show all possible values of x and the corresponding values of y. This is why the graph is a line and not just the dots that make up the points in our table. Now graph [latex]f(x)=3x+2[/latex]. Using the table of values we created above, you can think of f(x) as y. Each row forms an ordered pair that you can plot on a coordinate grid.
x f(x)
[latex]−2[/latex] [latex]−4[/latex]
[latex]−1[/latex] [latex]−1[/latex]
[latex]0[/latex] [latex]2[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]3[/latex] [latex]11[/latex]
Plot the points. The points negative 2, negative 4; the point negative 1, negative 1; the point 0, 2; the point 1, 5; the point 3, 11. Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge. A line through the points in the previous graph.   Let us try another one. Before you look at the answer, try to make the table yourself and draw the graph on a piece of paper.

Example

Graph [latex]f(x)=−x+1[/latex].

Answer: Start with a table of values. You can choose different values for x, but once again, it is helpful to include [latex]0[/latex], some positive values, and some negative values. If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid.

[latex]f(−2)=−(−2)+1=2+1=3\\f(−1)=−(−1)+1=1+1=2\\f(0)=−(0)+1=0+1=1\\f(1)=−(1)+1=−1+1=0\\f(2)=−(2)+1=−2+1=−1[/latex]

x f(x)
[latex]−2[/latex] [latex]3[/latex]
[latex]−1[/latex] [latex]2[/latex]
[latex]0[/latex] [latex]1[/latex]
[latex]1[/latex] [latex]0[/latex]
[latex]2[/latex] [latex]−1[/latex]
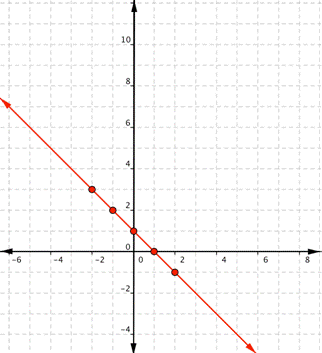
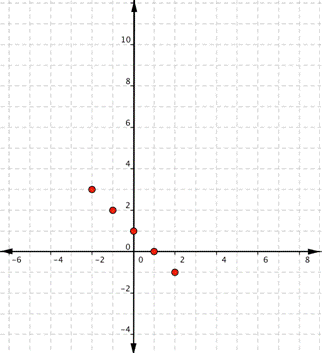Plot the points. The point negative 2, 3; the point negative 1, 2; the point 0, 1; the point 1, 0; the point 2, negative 1. Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge. Line through the points in the last graph.

The following video shows another example of how to graph a linear function on a set of coordinate axes. https://youtu.be/sfzpdThXpA8

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Ex: Graph a Linear Function Using a Table of Values (Function Notation). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Unit 17: Functions, from Developmental Math: An Open Program. . Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.