We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Absolute Value Functions

Learning Objectives

By the end of this lesson, you will be able to:
  • Graph an absolute value function.
  • Find the intercepts of an absolute value function
 
The Milky Way. Distances in deep space can be measured in all directions. As such, it is useful to consider distance in terms of absolute values. (credit: "s58y"/Flickr)
Until the 1920s, the so-called spiral nebulae were believed to be clouds of dust and gas in our own galaxy, some tens of thousands of light years away. Then, astronomer Edwin Hubble proved that these objects are galaxies in their own right, at distances of millions of light years. Today, astronomers can detect galaxies that are billions of light years away. Distances in the universe can be measured in all directions. As such, it is useful to consider distance as an absolute value function. In this section, we will investigate absolute value functions.

Understanding Absolute Value

Recall that in its basic form [latex]\displaystyle{f}\left({x}\right)={|x|}[/latex], the absolute value function, is one of our toolkit functions. The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign.

A General Note: Absolute Value Function

The absolute value function can be defined as a piecewise function

$latex f(x) = \begin{array}{l} x ,\ x \geq 0 \\ -x , x < 0\\ \end{array} $

Example: Determine a Number within a Prescribed Distance

Describe all values [latex]x[/latex] within or including a distance of 4 from the number 5.

Answer: Number line describing the difference of the distance of 4 away from 5. We want the distance between [latex]x[/latex] and 5 to be less than or equal to 4. We can draw a number line to represent the condition to be satisfied. The distance from [latex]x[/latex] to 5 can be represented using the absolute value as [latex]|x - 5|[/latex]. We want the values of [latex]x[/latex] that satisfy the condition [latex]|x - 5|\le 4[/latex].

Analysis of the Solution

Note that [latex-display]\displaystyle{-4}\le{x - 5}[/latex-display] [latex-display]\displaystyle{1}\le{x}[/latex-display] And: [latex-display]\displaystyle{x-5}\le{4}[/latex-display] [latex-display]\displaystyle{x}\le{9}[/latex-display] So [latex]|x - 5|\le 4[/latex] is equivalent to [latex]1\le x\le 9[/latex]. However, mathematicians generally prefer absolute value notation.

Try It

Describe all values [latex]x[/latex] within a distance of 3 from the number 2.

Answer: [latex-display]|x - 2|\le 3[/latex-display]

Q & A Do the graphs of absolute value functions always intersect the vertical axis? The horizontal axis? Yes, they always intersect the vertical axis. The graph of an absolute value function will intersect the vertical axis when the input is zero. No, they do not always intersect the horizontal axis. The graph may or may not intersect the horizontal axis, depending on how the graph has been shifted and reflected. It is possible for the absolute value function to intersect the horizontal axis at zero, one, or two points.
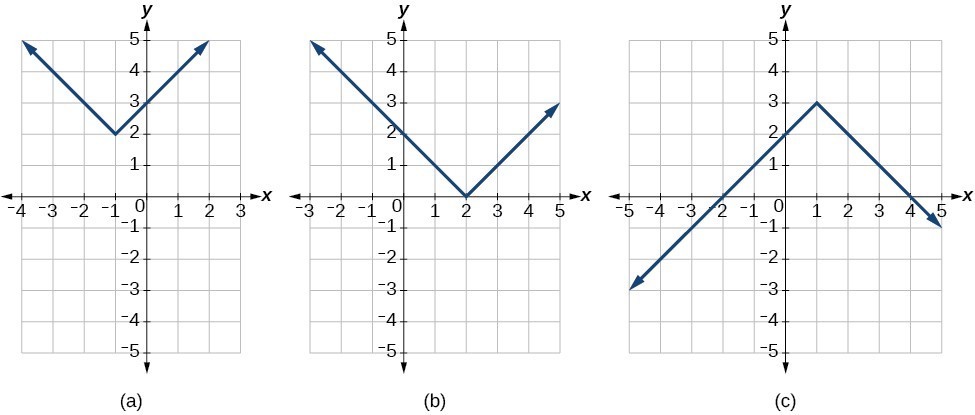Graph of the different types of transformations for an absolute function. (a) The absolute value function does not intersect the horizontal axis. (b) The absolute value function intersects the horizontal axis at one point. (c) The absolute value function intersects the horizontal axis at two points.

Find the Intercepts of an Absolute Value Function

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

How To: Given the formula for an absolute value function, find the horizontal intercepts of its graph.

  1. Isolate the absolute value term.
  2. Use [latex]|A|=B[/latex] to write [latex]A=B[/latex] or [latex]\mathrm{-A}=B[/latex], assuming [latex]B>0[/latex].
  3. Solve for [latex]x[/latex].

Example: Finding the Zeros of an Absolute Value Function

For the function [latex]f\left(x\right)=|4x+1|-7[/latex] , find the values of [latex]x[/latex] such that [latex]\text{ }f\left(x\right)=0[/latex] .

Answer:

[latex]\begin{array}{l}0=|4x+1|-7\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Substitute 0 for }f\left(x\right).\hfill \\ 7=|4x+1|\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \text{Isolate the absolute value on one side of the equation}.\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ 7=4x+1\hfill & \text{or}\hfill & \hfill & \hfill & \hfill & -7=4x+1\hfill & \text{Break into two separate equations and solve}.\hfill \\ 6=4x\hfill & \hfill & \hfill & \hfill & \hfill & -8=4x\hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ x=\frac{6}{4}=1.5\hfill & \hfill & \hfill & \hfill & \hfill & \text{ }x=\frac{-8}{4}=-2\hfill & \hfill \end{array}[/latex]

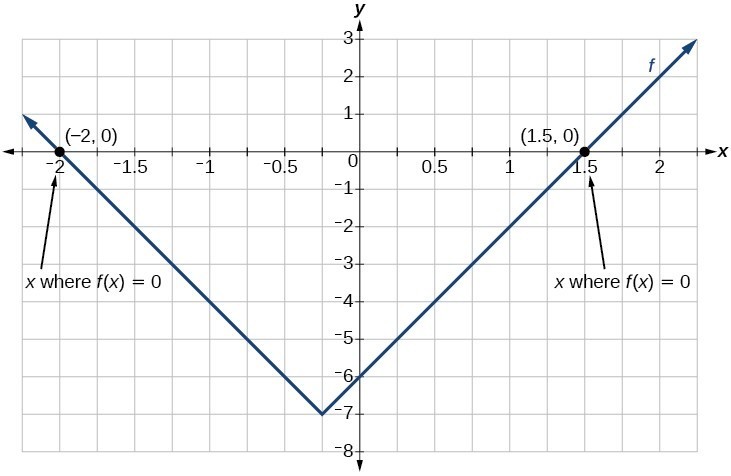Graph an absolute function with x-intercepts at -2 and 1.5. The function outputs 0 when [latex]x=1.5[/latex] or [latex]x=-2[/latex].

Try It

For the function [latex]f\left(x\right)=|2x - 1|-3[/latex], find the values of [latex]x[/latex] such that [latex]f\left(x\right)=0[/latex].

Answer: [latex]x=-1[/latex] or [latex]x=2[/latex]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 469. Authored by: WebWork-Rochester, mb Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 60791. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 40657. Authored by: Jenck,Michael. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.